This article is for those like me who haven't done GA (Genetic Algorithms) in a while, and need a refresher on the most common parent selection, crossover, and mutation algorithms.

I am limiting myself to those available in PyGAD, a nice Python library implementing GA. The knowledge can however be applied to other libraries/custom implementations as well, so keep reading!

A very quick reminder of how GA works

In a genetic algorithm, you start with an initial population of chromosomes, which are possible solutions to a given problem. Those chromosomes consist of an array of genes, that can be bits/ints/floats... You also specify a range of permissible values (e.g. integers from 0 to 9).

The whole optimization problem is encoded into a fitness function, which receives a chromosome and returns a number that tells the fitness (or goodness) of the solution. The higher the fitness, the better the solution encoded in the chromosome.

Then starts the loop. At each iteration (generation), a number of good chromosomes are selected for breeding (parent selection). Parents are combined two-by-two (crossover) to generate new chromosomes (children). The children are finally mutated by modifying somewhat randomly part of their genes, allowing for completely new solutions to emerge. The children go to the next generation and a new iteration starts (note that in some cases, it is possible to let some parents survive, see the keep_parents=N parameter in PyGAD).

The loop is stopped after a given number of generations (=iterations), or based on a stop criterion (for example, there is no improvement for a while).

PyGAD for GA

PyGAD is

an open-source Python library for building the genetic algorithm and optimizing machine learning algorithms.

It offers an implementation of genetic algorithm (GA) that is easy to use, yet powerful and flexible.

Here is an example of use by my dear friend @supcik:

---

Selection algorithms

The parent_selection_type defines the selection algorithm, that is which parents will be used for reproduction. At the time of writing, PyGAD supports 6 algorithms:

parent_selection_type="sss": The parent selection type. Supported types are sss (for steady-state selection), rws (for roulette wheel selection), sus (for stochastic universal selection), rank (for rank selection), random (for random selection), and tournament (for tournament selection).

Steady-state selection (sss, default)

Usually, the run of a genetic algorithm is divided into generations - at each generation, the result of the selection and reproduction process replaces all (or at least most) of the population; only children survive. In a steady-state genetic algorithm, however, only a few individuals are replaced at a time, meaning most of the individuals will carry out to the next generation; there is no generation per se.

There are multiple implementations. For example, in one variant, parents are selected using e.g. tournament selection. Then, children and parents are compared (based on the fitness value), and only the best ones are put back into the population.

In another variant, the best chromosomes are selected for reproduction, and their offspring will replace the worst individuals.

SSS is the only algorithm of this type offered by PyGAD at the time of writing.

→ See Wikipedia, StackOverflow: Genetic Algorithm - what is steady state selection?, cs.unm.edu

Roulette wheel selection (rws)

RWS is a fitness proportionate selection (FPS) algorithm, one of the most popular ways of parent selection.

In this family, each individual can become a parent with a probability proportional to his fitness. Choosing an individual can be depicted as spinning a roulette that has as many pockets as there are individuals in the current generation, with sizes depending on their probability. There is thus no strong guarantee of "survival of the fittest": good candidates can be eliminated, while the worst ones may survive.

The RWS variant is the simplest: each time a parent needs to be selected, the wheel is spun, meaning an individual can be selected multiple times, and the fittest have strong bias (= a very big chance to be drawn).

→ See Wikipedia, tutorialpoint

Stochastic universal sampling selection (sus)

SUS is another variant of fitness proportionate selection which exhibits no bias and minimal spread.

The same roulette wheel is used than in RWS, with the same proportions, but instead of using a single selection point and turning the roulette wheel again and again until all needed individuals have been selected, here, all the parents are selected at once. For that, the wheel is spun only once, and multiple selection points spaced evenly around the wheel determine which individuals are drawn.

This gives weaker members of the population (according to their fitness) a chance to be chosen, and also encourages the highly fit to be chosen at least once.

→ See Wikipedia, tutorialpoint, O'Reilly

Rank selection (rank)

The rank selection is useful when the population has very close fitness values. In this case, using a roulette wheel (RWS, SUS) would mean all individuals would basically have the same probability of being picked up... So instead, the idea is to base the probabilities not on the fitness value itself, but on the rank of the individual.

That is, we first rank the individuals from highest to lowest fitness value (i=1..N), assign the probabilities of being chosen based on sum of fitness values / i, and finally spin the wheel. Note that this would then be a linear rank selection: the ranks are in a linear progression. There are other schemes of rank selection, for example, exponential.

See Wikipedia, tutorialpoint, StackOverflow: matlab - random selection in GA?

Random selection (random)

The name says it all: the parents are randomly selected from the population, irrelevant of their fitness.

Tournament selection (tournament)

Tournament selection works by selecting K (tournament size) individuals randomly (tournament), and picking the fittest of them (the winner) for breeding.

The selection pressure depends on K: the largest K, the stronger the pressure, as weaker individuals will have more adversaries, and thus a higher chance of losing.

In PyGAD, the tournament size is controlled by the K_tournament parameter.

→ See Wikipedia, tutorialpoint

---

Crossover algorithms

The crossover_type defines how children are generated from the selected parents; in other words, how the reproduction works. At the time of writing, PyGAD supports 4 algorithms:

crossover_type="single_point": Type of the crossover operation. Supported types are single_point (for single-point crossover), two_points (for two points crossover), uniform (for uniform crossover), and scattered (for scattered crossover).

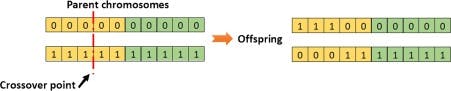
single-point crossover (single_point, default)

The breeding works by selecting an index randomly (crossover point). All genes to the right of that point are then swapped between the two parent chromosomes. This results in two offspring, each carrying some genetic information from both parents.

image source

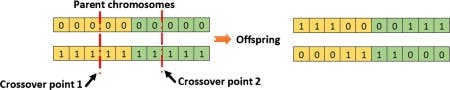
two-points crossover (two_points)

K-point crossover works the same as single-point crossover, but instead of one crossover point, we have many. PyGAD supports only K=2. In this case, the genes in between the two points are swapped between the parents, yielding again two new offspring.

image source

uniform crossover (uniform)

In a uniform crossover, we essentially flip a coin to decide whether each gene is left untouched, or taken from the other parent. In other words, each gene is chosen from either parent with equal probability. The technique is repeated for each new child.

Note that in some variants (but not PyGAD), it is possible to bias the coin towards one parent, resulting in children inheriting more from it.

image source

scattered crossover (scattered)

In scattered crossover, a random binary vector the size of the chromosomes is generated. The genes of the new child are taken from one parent when its index in the binary vector equals 0, and the other parent when it equals 1.

image source

---

Mutation algorithms

The mutation_types defines the mutation algorithm, that is which transformations are made to the children. It is possible to pass None, meaning no mutation. At the time of writing, PyGAD supports 5 algorithms:

mutation_type="random": Type of the mutation operation. Supported types are random (for random mutation), swap (for swap mutation), inversion (for inversion mutation), scramble (for scramble mutation), and adaptive (for adaptive mutation). It defaults to random.

The actual number of mutations applied to each child is controlled by the mutation_num_genes/mutation_probability/mutation_percent_genes parameters.

Here is the gist:

• random (default): a random value from the set of permissible values is assigned to a randomly chosen gene;

• swap: two genes are selected randomly and their values are swapped;

• inversion: a consecutive sequence of genes is selected, and their values reversed;

• scramble: as for inversion, a consecutive sequence of genes is selected, but this time their values are randomly shuffled;

• adaptive: apply a number of random mutations relative to the fitness of the individual. That is, children with a high fitness value will undergo fewer mutations than children with low fitness values. The actual variations are under your control, by specifying a lower and upper bound instead of a single value for mutation_num_genes/mutation_probability/mutation_percent_genes (see Using Adaptive Mutation in PyGAD). The idea behind it is straight-forward: altering good chromosomes has a high chance of degrading them, and vice-versa.

---

Written with ♡ by derlin